Context, Background, and Literature Review

Deliberative Control vs. Reactive Control

The traditional artificial intelligence (AI) approach to robot control is known as deliberative control. In this "sense-plan-act" control schema, the robot senses its environment and, based on a symbolic representation of that environment (i.e., world model), creates a plan to take the appropriate action [17; Fig. 4]. While the deliberative control architecture may be advantageous in a static, known environment, it is subject to failure in the presence of unforeseen events with respect to the world model.

Fig. 4: The "Sense-Plan-Act" Paradigm. [17]

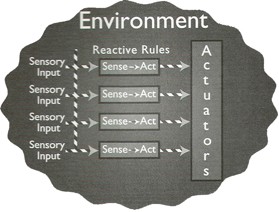
In contrast, a reactive system follows the "sense-act" paradigm, "tightly [coupling] perception to action without the use of intervening abstract representation or time history" [2, 17; Fig. 5]. Reactive control eliminates the need for a world model and traditional AI planning by, instead, relying on one or many simple behaviors [2, 5].

Fig. 5: The "Sense-Act" Paradigm. [17]

Swarms vs. Formations

Seminal work by C. Reynolds [21] applies reactive control structures to show how individuals can exhibit emergent aggregate behavior similar to flocking birds. In this work, simulated birds alter their movement in three-dimensional space based on the direction, pitch, yaw, velocity, and distance of their neighbors. Flocking algorithms have been used for both physical [13] and simulated robots [1]. Distributed control methods based on gravitational physics [25] and gas particle interactions [6] have generated emergent structures. A digital hormone model, inspired by biological cell interaction, has also been proposed for robotic organization [24]. However, these apply more to swarms as opposed to formations, where a swarm is defined as a massive collection that moves with no group organization, much like a swarm of bees or a flock of birds [Fig. 6].

Fig. 6: Flock of Birds Demonstrating Swarm-Like Behavior. Note the Lack of Organization.

While a formation is similar, the distinction is made in that it maintains a global structure, much like a flock of geese or a marching band [Fig. 7 & 8]. Robot formations have been applied to applications such as automated traffic cones [9], while swarm behavior control has been applied to urban search-and-rescue robotics [27].

Fig. 7: Flock of Geese in Formation. Fig. 8: Marching Band Formation, Demonstrating and Maintaining Well-Defined Organization.

Robots capable of attaching to one another have been proposed for formation applications. Tethered formation flight has been implemented on small robotic satellites in the SPHERES project [22; Fig. 9]. By keeping each tether taut, these robots are able to preserve their organization. Related work utilizes electromagnets and a reaction wheel to control the position and orientation of a robot relative to another [14], but is currently limited in the number of units that can be controlled.

Fig. 9: Three SPHERES Satellites Maintain Formation by Keeping their Tethers Taut.

In [12], robots autonomously self-assemble into a single robotic configuration. These "swarm-bots" only interact with and connect to robots in their immediate vicinity and, thus, are able to self-organize without using a global coordination system [Fig. 10]. These types of strict connections make for a strong structure, but are rather restricted in their ability to change configurations. The challenges for applying a robot formation approach to SSP include generalizing the formation process, increasing the size of the robot formation, and formation management.

Fig. 10: Independent "Swarm-Bots" (Indicated by Blue Lights; Left) Connect with Others (Indicated by Red Lights; Right).

Previous work on maintaining formation has been applied on up to a dozen physical robots [20]; however, to better demonstrate group behavior on a larger scale, the number of mobile units must be increased. For a formation of robots numbering in the thousands, such as the 33,000 robots that Landis [15] projected would be needed for SSP, direct control through a remote teleoperation interface, in which an operator or a small group of operators must take control of each individual robot, is impractical. Rather, the robot formation will require some level of autonomous control. Computationally, the simplest robot control strategy is a form of reactive control where, in the case of formations, each robot responds to changes in its local neighborhood. It has the advantage of eliminating the need for each robot to maintain information about the global or overall structure of the entire formation.

This approach to the autonomous control of creating and maintaining multi-robot formations is similar to work done in coordinating formations of Earth-bound, mobile robots [3, 10, 11, 31]. Inspired by biological or organizational systems, such as the flight patterns of geese, Fredslund & Mataric [10, 11] assign a particular formation for robots to follow, such as a line, a V-shape, or a diamond [Fig. 11]. Each robot is given and transmits a position in the formation, an identification number, and the color of its corresponding "helmet". Using a combination of laser sensors, color tracking, and robot intercommunication, each robot is able to identify its "friend" (neighbor to reference). A robot leader is designated that transmits the specified formation. When the leader moves, neighboring robots adjust their orientation appropriately. In this way, the robot group is able to maintain a stable formation. However, this will only occur if the formation is moving; if the formation is not moving, robots are only able to determine their distance to their corresponding friend—true orientation is unknown. Because the robots are forced to move, an emergent restriction is imposed on the system: robots must follow (i.e., stay behind) their friend. Thus, formations are limited to those of non-frontal concavities with respect to the leading robot.

Fig. 11: An Overhead View of 4 Mobile Robots Traveling in a Diamond Formation. [10]

World-Space Cellular Automata vs. Robot-Space Cellular Automata

Utilizing reactive control techniques similar to flocking, Dudenhoeffer & Jones [8] demonstrate (in simulation) emergent robot organization in an environment that has been broken down into a 2-dimensional cellular automaton. A cellular automaton consists of a chain (1-dimensional) or lattice (2-or-3-dimensional) of computational cells, each cell being in one of a given set of states that evolve through discrete time steps [29]. The dynamic behavior of the automaton is determined by a set of rules that govern the change of state of an individual cell with respect to its neighbors.

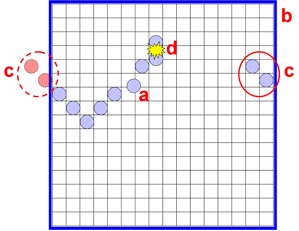
Many practical implications must be considered when a given environment is represented topologically as a cellular automaton—referred to henceforth as a world-space cellular automaton [Fig. 12]. The next state of a robot within some cell depends solely on the occupancy state of cells within its neighborhood, which consists of the cell that the robot is currently in, as well as surrounding cells. This imposes strict limitations on the system. First, a robot must only occupy a single cell at any given time [Fig. 12a]. As robot movement is often inaccurate, this restriction can be difficult to satisfy without some form of external localization within the environment. Second, the robot must be bound to occupy only cells defined within the world-space. Thus, boundaries must be specified [Fig. 12b]. Moreover, rules for cells on the borders of a simulated automaton may allow for a type of wrapping to the opposing side to ensure proper neighborhood size [Fig. 12c]; however, in a physical implementation this is not feasible. Instead, specific rules must be in place for dealing with these boundary cells. Finally, many of the cells will be unoccupied, which, based on the specified rule set, has an effect on the next state of a robot. This increases the risk of collisions when two robots attempt to move to the same unoccupied grid cell [Fig. 12d]. Communication between robots would alleviate this, but would violate inherent restrictions in cellular automata if communication extends behind that of the neighborhood.

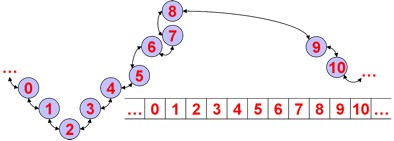
Fig. 12: Illustrates Various Limitations of 2-dimensional World-Space Cellular Automata: (a) Robot is between Grid Cells; (b) Boundary Surrounds the Automaton; (c) Automaton Wraps along Boundaries; (d) Two Robots Collide while Trying to Occupy the Same Grid Cell.

In keeping with a simple reactive control strategy, the approach of Mead et al. [19, 20] is to treat the robots in the formation as cells in a 1-dimensional robot-space cellular automaton [Fig. 13]. This distinguishes itself in that the actual robots that make up the global structure (i.e., not the structure itself) are represented by the cells. This approach overcomes many of the limitations inherent in a world-space automaton, eliminating the dependence on the environment and reducing the complexity of the automaton.

Fig. 13: Robots as Cells in a 1-Dimensional Robot-Space Cellular Automaton.

Each robot "cell state" consists of its desired and actual spatial orientation in 2-dimensional space in relation to neighboring robots. The robot's behavior is governed by a set of rules for changing its state with respect to its neighbors. By designating a single robot as a "seed" or "initiator" cell of the formation, human intervention can change its orientation directly. This causes a type of chain reaction in the formation by each individual robot, which applies behavior rules based on the change in states of its neighbors. This is analogous to seeing a crowd in a baseball stadium "doing the wave", where each individual's reaction in the crowd is based solely on the people sitting nearby. The formation algorithm was initially implemented in simulation [19]. The simulator demonstrated the scalability and generality of the system, with over 3,000 agents conforming to a variety of different formations. In 2007, the feasibility of the approach was demonstrated on a physical platform [20; Fig. 14].

Fig. 14: Eleven Robots in a Parabolic Formation.

References
  1. Ando, K., Suzuki, I., & Yamashita, M. (1995). Formation and Agreement Problems for Synchronous Mobile Robots with Limited Visibility. Proceedings of the IEEE International Symposium on Intelligent Control, Monterey, California, 453-460.
  2. Arkin, R. (1998). Behavior-Based Robotics, The MIT Press, Cambridge, Massachusetts.
  3. Balch, T. & Arkin, R. (1998). Behavior-based Formation Control for Multi-Robot Teams. IEEE Transactions on Robotics and Automation, 14(6), 926-939.
  4. Bekey, G., Bekey, I., Criswell, D., Friedman, G., Greenwood, D., Miller, D., & Will, P. (2000). Final Report of the NSF-NASA Workshop on Autonomous Construction and Manufacturing for Space Electrical Power Systems. 4-7 April, Arlington, Virginia.
  5. Brooks, R.A. & Flynn, A.M. (1989). Fast, Cheap, and Out of Control: A Robot Invasion of the Solar System. Journal of the British Interplanetary Society, 42(10), 478-485.
  6. Cheng, J., Cheng, W., & Nagpal, R. (2005) Robust and Self-repairing Formation Control for Swarms of Mobile Agents. In the Proceedings of The 20th National Conference on Artificial Intelligence (AAAI-05), 59-64. Pittsburgh, Pennsylvania.
  7. Clynes, T. (2006). The Energy Fix: 10 Steps to End America's Fossil Fuel Addiction. Popular Science, July 2006: 47-60.
  8. Dudenhoeffer, D.D. & Jones, M.P. (2000). A Formation Behavior for Large-Scale Micro-Robot Force Deployment. Proceedings of the 2000 Winter Simulation Conference, 972-982.
  9. Farritor, S.M. & Goddard, S. (2004). Intelligent Highway Safety Markers. IEEE Intelligent Systems, 19(6), 8-11.
  10. Fredslund, J. & Mataric, M.J. (2002). Robots in Formation Using Local Information. The 7th International Conference on Intelligent Autonomous Systems, Marina del Rey, California.
  11. Fredslund, J. & Mataric, M.J. (2002). A General Algorithm for Robot Formations Using Local Sensing and Minimal Communication. IEEE Proceedings on Robotics and Automation, 18(5).
  12. Groß, R., Bonani, M., Mondada, F., & Dorigo, M. (2006). Autonomous Self-Assembly in Swarm-Bots. IEEE Transactions on Robotics, 22(6).
  13. Kelly, I.D. & Keating, D.A. (1996). Flocking by the Fusion of Sonar and Active Infrared Sensors on Physical Autonomous Mobile Robots. The 3rd International Conference on Mechatronics and Machine Vision in Practice, 1-4. Guimaraes, Portugal.
  14. Kong, E.M.C., Kwon, D.W., Schweighart, S.A., Elias, L.M., Sedwick, R.J., Miller, D.W., (2004). Electromagnetic Formation Flight for Multisatellite Arrays. AIAA Journal of Spacecraft and Rockets, 41(4), 659-666.
  15. Landis, G. (2004). Reinventing the Solar Power Satellite. The 53rd International Astronautical Congress, Houston, Texas.
  16. Mankins, J.C. (1997). A Fresh Look at Space Solar Power: New Architectures, Concepts and Technologies. IAF-97-R.2.03, 38th International Astronautical Federation.
  17. Mataric, M.J. (2007). The Robotics Primer, The MIT Press, Cambridge, Massachusetts.
  18. McLurkin, J.D. (2004). Stupid Robot Tricks: A Behavior-Based Distributed Algorithm Library for Programming Swarms of Robots. Master's Thesis, Massachusetts Institute of Technology.
  19. Mead, R. & Weinberg, J.B. (2006). Algorithms for Control and Interaction of Large Formations of Robots. In the Proceedings of The 21st National Conference on Artificial Intelligence (AAAI-06), 1891-1892. Boston, Massachusetts.
  20. Mead, R., Weinberg, J.B., & Croxell, J.R. (2007). A Demonstration of a Robot Formation Control Algorithm and Platform. To appear in the Proceedings of Robot Competition and Exhibition of The 22nd National Conference on Artificial Intelligence (AAAI-07), Vancouver, British Columbia.
  21. Reynolds, C.W. (1987). Flocks, Herds, and Schools: A Distributed Behavioral Model, in Computer Graphics. SIGGRAPH '87 Conference Proceedings, 21(4), 25-34.
  22. Saenz-Otero, A. & Miller, D.W., (2005). SPHERES: A Platform for Formation-flight Research. UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts II Conference, San Diego, California.
  23. Sarkar, P. (2000). A Brief History of Cellular Automata. ACM Computing Surveys, 32(1), 80-107.
  24. Shen, W., Will, P., Galstyan, A., & Chuong, C. (2004). Hormone-Inspired Self-Organization and Distributed Control of Robotic Swarms. Autonomous Robots, 17, 93-105.
  25. Skubic, M., Anderson, D., Khalilia, M., & Kavirayani, S. (2004). A Sketch-Based Interface for Multi-Robot Formations. AAAI Mobile Robot Competition 2004: Papers from the AAAI Workshops, San Jose, California.
  26. Spears, W.M., Spears, D.F., Hamann, J.C., & Hill, R. (2004). Distributed, Physics-Based Control of Swarms of Vehicles. Autonomous Robots, (17), 137-162.
  27. Tejada, S., Cristina, A., Goodwyne, P., Normand, E., O'Hara, R., & Tarapore, S. (2003). Virtual Synergy: A Human-Robot Interface for Urban Search and Rescue. In the Proceedings of the AAAI 2003 Robot Competition, Acapulco, Mexico.
  28. Wessnitzer, J. Adamatzky, A. & Melhuish, C. (2001). Towards Self-Organising Robot Formations: A Decentralised Approach. Proceedings of the European Conference on Artificial Life.
  29. Wolfram, S. (2002). A New Kind Of Science, Wolfram Media.
  30. XBee™/XBee-PRO™ OEM RF Modules. (2006). Product Manual v1.x8x - 802.15.4 Protocol, MaxStream, Inc.
  31. Yamaguchi, H., Arai, T., & Beni, G. (2001). A Distributed Control Scheme for Multiple Robotic Vehicles to Make Group Formation, Robotics and Autonomous Systems, (36), 125-147.